精华 图算法系列《第八章 用图算法增强机器学习-2》
发布于 5 年前 作者 feng_neo4j 1764 次浏览 来自 分享

对图算法有兴趣的朋友可以关注微信公众号 ：《 Medical与AI的故事》

原文链接：《图算法》第八章-2 用图算法增强机器学习

均衡和拆分数据

两个节点之间的CO_AUTHOR_EARLY和CO_AUTHOR_LATE关系将作为我们的积极（positive）例子，但我们也需要创建一些消极（negative）的例子。大多数现实世界中的网络都是稀疏的，只有局部密集，这个图也是这样。两个节点没有关系的样本数比有关系的样本数大得多。

如果我们查询我们的CO_AUTHOR_EARLY数据，我们会发现有45,018个作者有这种关系，但只有81,096个协作关系。这听起来可能不平衡，但事实更加严峻：我们的图可能具有的最大关系数是（45,018*45,017）/2=1,013,287,653，这意味着有很多负面的例子（没有链接）。如果我们用所有的负面例子来训练我们的模型，我们将有一个严重的类不平衡问题(class imbalance problem)。一个模型可以通过预测每对节点都没有关系来达到极高的精度。

在R. Lichtenwalter、J. Lussier和N. Chawla的论文“New Perspectives and Methods in Link Prediction”中，描述了解决这一挑战的几种方法。其中一种方法是通过在我们的邻近节点中找到我们当前没有连接的节点来构建负面的例子。

我们将通过找到两个到三个跃点之间的混合节点对来构建我们的负面示例，不包括那些已经有关系的节点对。然后我们将对这些节点对进行降采样，这样我们就可以得到等量的正负示例。 在这里插入图片描述 我们有314,248对节点，它们在两个跃点之间没有关系。如果我们增加距离到三个跃点，我们有967,677对节点。 下面的函数将用于对负面样本进行降采样：

def down_sample(df):
    copy = df.copy()
    zero = Counter(copy.label.values)[0]
    un = Counter(copy.label.values)[1]
    n = zero - un
    copy = copy.drop(copy[copy.label == 0].sample(n=n, random_state=1).index)
    return copy.sample(frac=1)

这个函数计算出正负两个例子的数量之差，然后对负的例子进行采样，从而得到相等的数字。然后，我们可以运行以下代码来构建一个具有平衡的正负示例的训练集：

train_existing_links = graph.run("""
MATCH (author:Author)-[:CO_AUTHOR_EARLY]->(other:Author)
RETURN id(author) AS node1, id(other) AS node2, 1 AS label
""").to_data_frame()
train_missing_links = graph.run("""
MATCH (author:Author)
WHERE (author)-[:CO_AUTHOR_EARLY]-()
MATCH (author)-[:CO_AUTHOR_EARLY*2..3]-(other)
WHERE not((author)-[:CO_AUTHOR_EARLY]-(other))
RETURN id(author) AS node1, id(other) AS node2, 0 AS label
""").to_data_frame()
train_missing_links = train_missing_links.drop_duplicates()
training_df = train_missing_links.append(train_existing_links, ignore_index=True)
training_df['label'] = training_df['label'].astype('category')
training_df = down_sample(training_df)
training_data = spark.createDataFrame(training_df)

我们现在将label列强制（coerce）为一个类别，其中1表示一对节点之间存在链接，0表示没有链接。我们可以通过运行以下代码来查看DataFrame中的数据：

training_data.show(n=5)
+-------+-------+-------+
| node1 | node2 | label |
+-------+-------+-------+
| 10019 | 28091 | 1     |
| 10170 | 51476 | 1     |
| 10259 | 17140 | 0     |
| 10259 | 26047 | 1     |
| 10293 | 71349 | 1     |
+-------+-------+-------+

结果向我们展示了节点对的列表，以及它们是否具有合著者关系；例如，节点10019和28091具有1个标签，表示有一个协作。 现在，让我们执行以下代码来检查DataFrame的内容摘要：

training_data.groupby("label").count().show()

结果如下：

+-------+-------+
| label | count |
+-------+-------+
| 0     | 81096 |
| 1     | 81096 |
+-------+-------+

我们用相同数量的positive和negative样本创建了我们的训练集。现在我们需要为测试集做同样的事情。以下代码将使用平衡的正负示例构建测试集：

test_existing_links = graph.run("""
MATCH (author:Author)-[:CO_AUTHOR_LATE]->(other:Author)
RETURN id(author) AS node1, id(other) AS node2, 1 AS label
""").to_data_frame()
test_missing_links = graph.run("""
MATCH (author:Author)
WHERE (author)-[:CO_AUTHOR_LATE]-()
MATCH (author)-[:CO_AUTHOR*2..3]-(other)
WHERE not((author)-[:CO_AUTHOR]-(other))
RETURN id(author) AS node1, id(other) AS node2, 0 AS label
""").to_data_frame()
test_missing_links = test_missing_links.drop_duplicates()
test_df = test_missing_links.append(test_existing_links, ignore_index=True)
test_df['label'] = test_df['label'].astype('category')
test_df = down_sample(test_df)
test_data = spark.createDataFrame(test_df)

我们可以执行如下代码来查看DataFrame的内容：

test_data.groupby("label").count().show()

结果如下：

+-------+-------+
| label | count |
+-------+-------+
| 0     | 74128 |
| 1     | 74128 |
+-------+-------+

既然我们已经平衡了训练和测试数据集，那么让我们看看预测链接的方法。

如何预测缺少的链接

我们需要从一些基本假设开始，即数据中的哪些元素可以预测两位作者是否会在以后成为合著者。我们的假设因领域和问题而异，但在这种情况下，我们相信最具预测性的特征将与社区有关。我们将从以下假设开始，即以下要素增加了作者成为合著者的可能性：（猜想一些特征与最终的结果相关）

  • 更多共同作者
  • 作者之间潜在的三元关系
  • 有更多任意类型关系的作者
  • 同一社区的作者（这里的社区指的是community detection算法中的社区，并非物理上的实际的社区，下同）
  • 同一个更紧密社区的作者

我们将基于我们的假设构建图特征，并使用这些特征训练二元分类器。二元分类是一种ML类型，其任务是根据规则预测元素所属的两个预定义组中的哪一个。我们使用分类器来根据分类规则预测一对作者是否有链接。对于我们的示例，值1表示有一个链接（有合著者关系），值0表示没有链接（没有合著者关系）。

我们将利用Spark中的随机森林实现我们的分类器。随机森林是一种用于分类、回归和其他任务的集成学习方法，如图8-7所示。 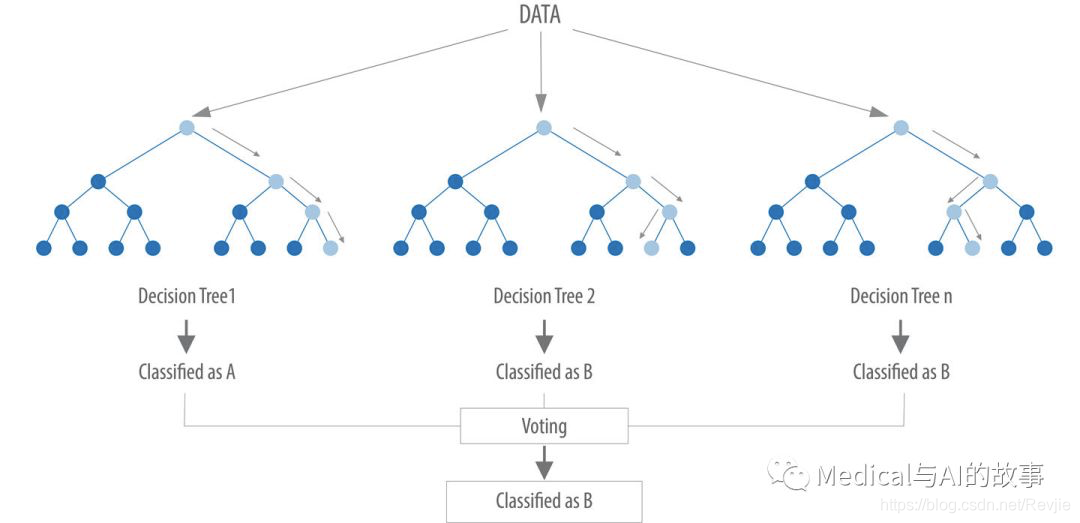在这里插入图片描述 图8-7.一个随机森林建立一个决策树集合，然后将结果聚合为多数票（用于分类）或平均值（用于回归）。 我们的随机森林分类器将从我们训练的多个决策树中获取结果，并使用投票来预测分类。在这里的例子中，分类意味着是否存在链接（合著者关系）。现在让我们创建我们的工作流程。

创建机器学习的管道

我们将基于Spark中的随机森林分类器创建机器学习管道。这种方法非常适合，因为我们的数据集将由强特征(对结果影响较大的特征)和弱特征混合组成。虽然弱特征有时会有所帮助，但随机森林方法将确保我们不会创建只适合我们的训练数据的模型。

为了创建我们的ML管道（pipline），我们将传入一个特征列表作为字段变量，这些是我们的分类器将使用的特征。分类器期望将这些特征接收为一个单独的列features，因此我们使用VectorAssembler来将数据转换为所需的格式。

以下代码创建机器学习管道，并使用MLLib设置参数：

def create_pipeline(fields):
    assembler = VectorAssembler(inputCols=fields, outputCol="features")
    rf = RandomForestClassifier(labelCol="label", featuresCol="features",
                                numTrees=30, maxDepth=10)
    return Pipeline(stages=[assembler, rf])

RandomForestClassifier使用以下参数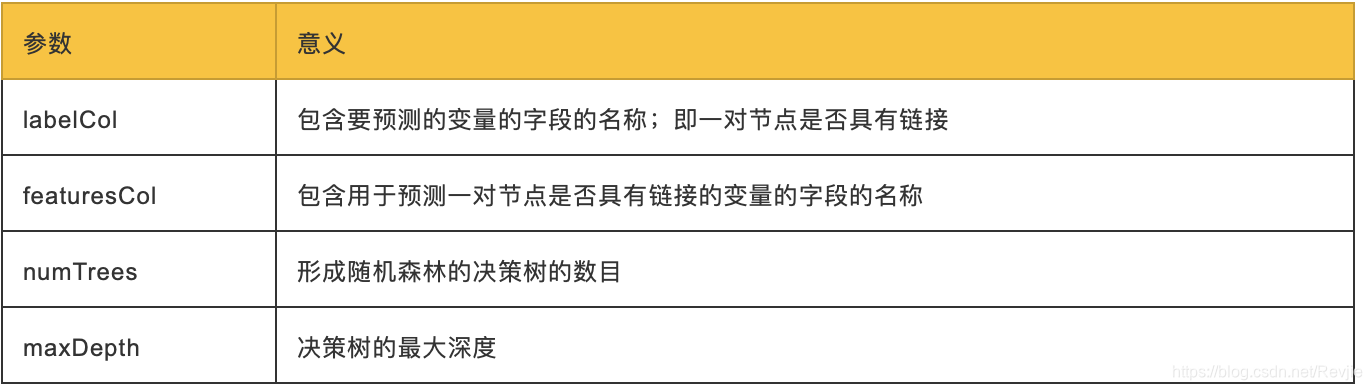： 在这里插入图片描述 我们根据实验选择决策树的数量和深度。我们可以考虑超参数，比如可以调整以优化性能的算法设置。最佳超参数通常很难提前确定，而调整模型通常需要一些尝试和错误。

我们已经介绍了基础知识并建立了我们的管道，所以让我们开始创建模型并评估它的性能。

预测链接：基本的图特征

我们将首先创建一个简单的模型，该模型试图根据两位作者的Common authors、preferential attachment和the total union of neighbors中提取的特征来预测未来的协作：

  • Common authors：查找两个作者之间的潜在三角形数。这抓住了这样一个观点，即两个有共同作者的作者将来可能会被介绍和合作。
  • Preferential attachment（择优附着）通过将每对作者的合著者数量相乘，为每对作者生成一个分数。直觉是已经和其他人合作的作者更有可能开展合作。
  • Total union of neighbors：查找每个作者的合著者总数，减去重复项。 在Neo4j中，我们可以使用Cypher查询计算这些值。以下函数将计算训练集的这些度量：
def apply_graphy_training_features(data):
    query = """
    UNWIND $pairs AS pair
    MATCH (p1) WHERE id(p1) = pair.node1
    MATCH (p2) WHERE id(p2) = pair.node2
    RETURN pair.node1 AS node1,
            pair.node2 AS node2,
            size([(p1)-[:CO_AUTHOR_EARLY]-(a)-
                        [:CO_AUTHOR_EARLY]-(p2) | a]) AS commonAuthors,
            size((p1)-[:CO_AUTHOR_EARLY]-()) * size((p2)-
                        [:CO_AUTHOR_EARLY]-()) AS prefAttachment,
            size(apoc.coll.toSet(
                [(p1)-[:CO_AUTHOR_EARLY]-(a) | id(a)] +
                    [(p2)-[:CO_AUTHOR_EARLY]-(a) | id(a)]
            )) AS totalNeighbors
    """
    pairs = [{"node1": row["node1"], "node2": row["node2"]}
                                    for row in data.collect()]
    features = spark.createDataFrame(graph.run(query,
                                    {"pairs": pairs}).to_data_frame())
    return data.join(features, ["node1", "node2”])

下面的函数将为测试集计算它们：

def apply_graphy_test_features(data):
    query = """
    UNWIND $pairs AS pair
    MATCH (p1) WHERE id(p1) = pair.node1
    MATCH (p2) WHERE id(p2) = pair.node2
    RETURN pair.node1 AS node1,
            pair.node2 AS node2,
            size([(p1)-[:CO_AUTHOR]-(a)-[:CO_AUTHOR]-(p2) | a]) AS commonAuthors,
            size((p1)-[:CO_AUTHOR]-()) * size((p2)-[:CO_AUTHOR]-())
                        AS prefAttachment,
            size(apoc.coll.toSet(
                [(p1)-[:CO_AUTHOR]-(a) | id(a)] + [(p2)-[:CO_AUTHOR]-(a) | id(a)]
                )) AS totalNeighbors
    """
    pairs = [{"node1": row["node1"], "node2": row["node2"]}
                                for row in data.collect()]
    features = spark.createDataFrame(graph.run(query,
                                    {"pairs": pairs}).to_data_frame())
    return data.join(features, ["node1", "node2”])

这两个函数都采用一个DataFrame，其中包含列node1和node2中的节点对。然后我们构建一个包含这些对的映射数组，并计算每对节点的每个度量值。 在这里插入图片描述 在本章中，UNWIND子句对于获取大量节点对的集合，并在一个查询中返回它们的所有特征特别有用。 我们可以在Spark中使用以下代码将这些功能应用于我们的训练和测试数据帧：

training_data = apply_graphy_training_features(training_data)
test_data = apply_graphy_test_features(test_data)

让我们来探索一下我们训练集中的数据。以下代码将绘制commonAuthors频率的柱状图：

plt.style.use('fivethirtyeight')
fig, axs = plt.subplots(1, 2, figsize=(18, 7), sharey=True)
charts = [(1, "have collaborated"), (0, "haven't collaborated”)]
for index, chart in enumerate(charts):
    label, title = chart
    filtered = training_data.filter(training_data["label"] == label)
    common_authors = filtered.toPandas()["commonAuthors"]
    histogram = common_authors.value_counts().sort_index()
    histogram /= float(histogram.sum())
    histogram.plot(kind="bar", x='Common Authors', color="darkblue",
                    ax=axs[index], title=f"Authors who {title} (label={label})")
    axs[index].xaxis.set_label_text("Common Authors")
plt.tight_layout()
plt.show()

我们可以看到图8-8中的图表。 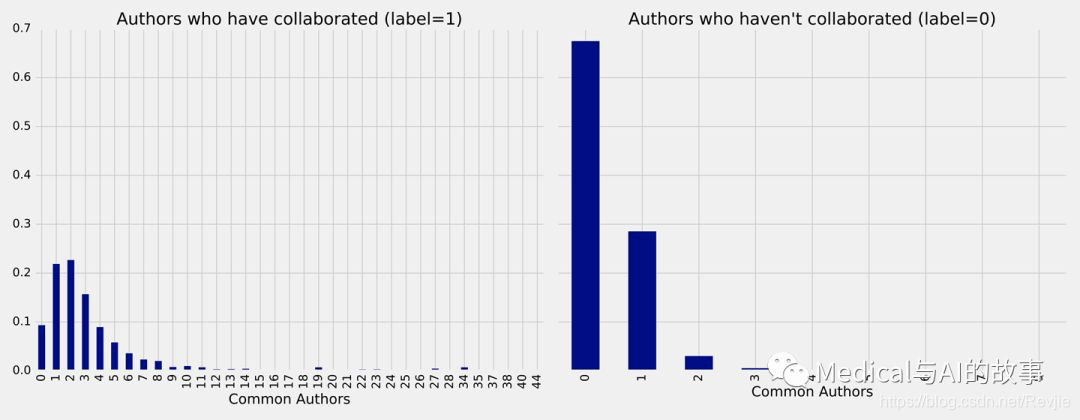在这里插入图片描述 图8-8.commonAuthors的频率

左边是作者之间有合作时的commonAuthors频率，右边是没有合作时的commonAuthors频率。没有合作的commonAuthors的最大数量为9，但95%的值是1或0。这不奇怪，在那些没有合作过的人中，大多数人之间也没有其他的共同作者。对于那些合作过的人（左边），70%有少于5个共同作者，以有1~2个共同作者的情况居多。

现在我们要训练一个模型来预测丢失的链接。以下函数执行此操作：

def train_model(fields, training_data):
    pipeline = create_pipeline(fields)
    model = pipeline.fit(training_data)
    return model

我们将首先创建一个只使用commonAuthors的基本模型。我们可以通过运行以下代码来创建该模型：

basic_model = train_model(["commonAuthors"], training_data)

在我们的模型经过训练后，让我们检查它如何与一些dummy数据进行比较。以下代码根据commonAuthors的不同值评估代码：

eval_df = spark.createDataFrame(
    [(0,), (1,), (2,), (10,), (100,)],
    ['commonAuthors'])
(basic_model.transform(eval_df)
.select("commonAuthors", "probability", "prediction")
.show(truncate=False))

运行该代码将得到以下结果：

+---------------+------------------------------------------+------------+
| commonAuthors | probability                              | prediction |
+---------------+------------------------------------------+------------+
| 0             | [0.7540494940434322,0.24595050595656787] | 0.0        |
| 1             | [0.7540494940434322,0.24595050595656787] | 0.0        |
| 2             | [0.0536835525078107,0.9463164474921892]  | 1.0        |
| 10            | [0.0536835525078107,0.9463164474921892]  | 1.0        |
+---------------+------------------------------------------+------------+

如果我们的commonAuthors值小于2，有75%的概率作者之间不会有关系，所以我们的模型预测为0。如果我们的commonAuthors值为2或更大，则94%的概率表示作者之间存在关系，因此我们的模型预测1。

回到顶部