精华 图算法系列《第六章 社区检测算法-1》
发布于 5 年前 作者 feng_neo4j 3437 次浏览 来自 分享

对图算法有兴趣的朋友可以关注微信公众号 ：《 Medical与AI的故事》

原文链接：《《图算法》第六章-1 社区检测算法

形成一个社区在所有类型的网络中都很常见，识别它们对于评估群体行为和突发现象都很重要。通常来说，社区的成员在群体内的关系比在群体外的节点多，这是社区检测的一般原则。识别这些相关集体可以揭示节点群集、独立组和网络结构。此信息有助于推断对等的各组的相似行为和偏好、弹性估算和查找嵌套关系，也可以为其他分析准备数据。社区检测算法也常用于生成用来做一般性检测的网络可视化图。

我们将提供最具代表性的社区检测算法的详细信息，包括：

  • 计算整体关系密度的三角形计数(Triangle Count)和聚类系数（Clustering Coefficient）
  • 用于查找连接聚类的强连接组件（Strongly Connected Components）和连接组件(Connected Components)
  • 基于节点标签快速推断分组的标签传播(Label Propagation)
  • 用于查看分组品质和层次结构的Louvain模块化算法（Louvain Modularity） 我们将解释这些算法是如何工作的，并在Apache Spark和Neo4j中运行示例。如果一个算法只在一个平台上可用，我们将只提供一个示例。在这些算法中，我么使用带有权重的关系，因为这些算法通常用于捕获不同关系的重要性。

图6-1概述了这里介绍的社区检测算法之间的差异，表6-1提供了每个算法计算什么，以及示例用法。 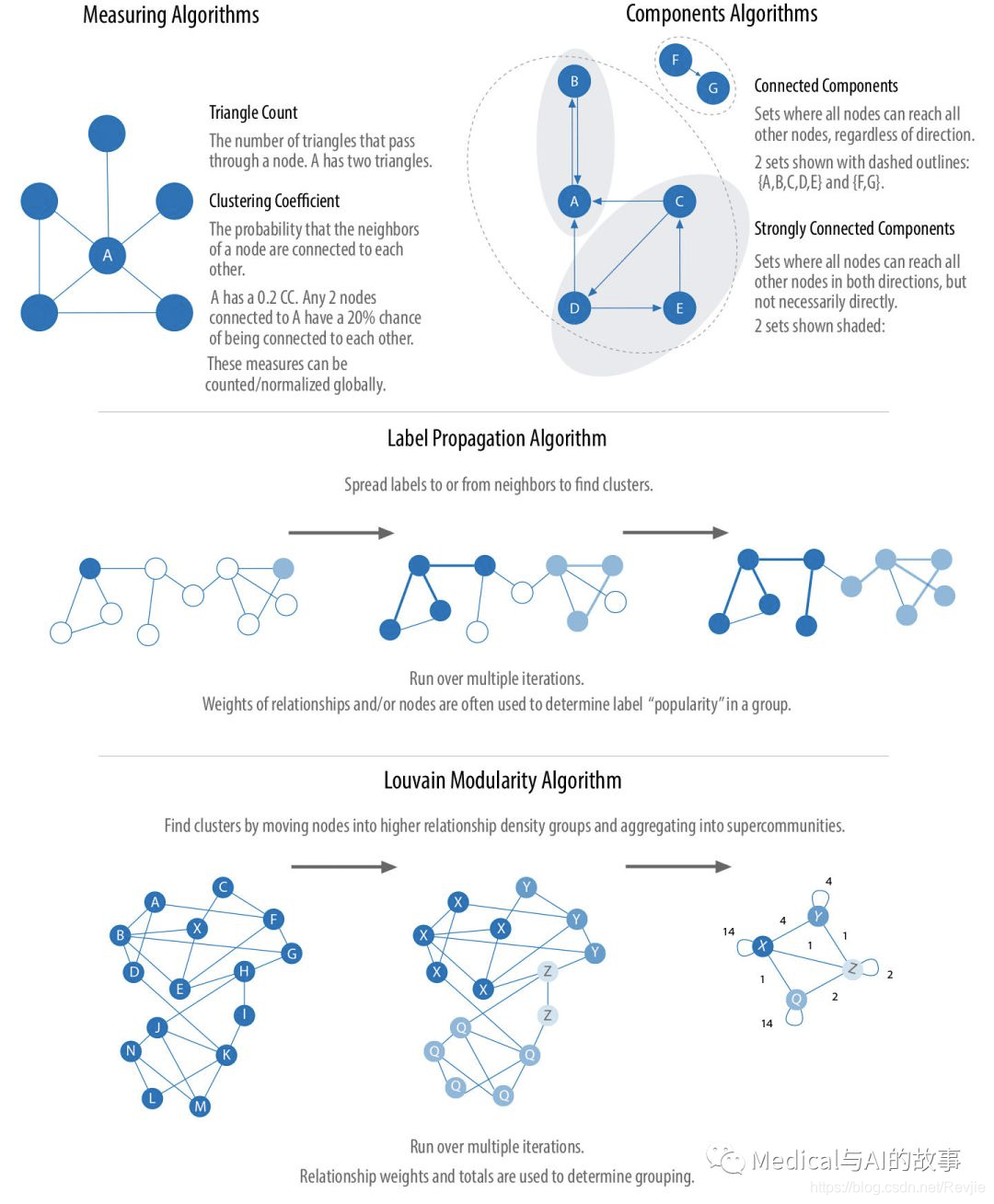在这里插入图片描述 图6-1.典型的社区检测算法 在这里插入图片描述 我们会使用以下的可相互替换的术语：集（set）、分区（partition）、集群（cluster）、组（group）和社区（community）。它们表达的都是，节点可以被分组。社区检测（community detection）算法也称为聚类（clustering）和分区（partitioning）算法。在每一部分中，我们使用文献中最突出的那个术语来描述这个算法。

表6-1.社区检测算法综述 在这里插入图片描述 首先，我们将描述示例使用的数据，并将数据导入Spark和Neo4j。算法按表6-1中列出的顺序进行介绍。对于每一个算法，你将找到一个简短的描述和建议，关于何时使用它。大多数章节还包括有关何时使用相关算法的指导。我们在每个算法部分的末尾使用示例数据来演示示例代码。 在这里插入图片描述 当使用社区检测算法时，要注意关系的密度。如果图非常密集，那么最终可能会导致所有节点聚集在一个或几个集群中。你可以通过度、关系权重或相似性度量的过滤来缓解这一点。 另一方面，如果图太稀疏，连接的节点很少，那么您可能会得到每个聚类只有一个节点。在这种情况下，尝试合并进来更多相关信息和其他关系类型。

图数据示例：软件依赖关系图

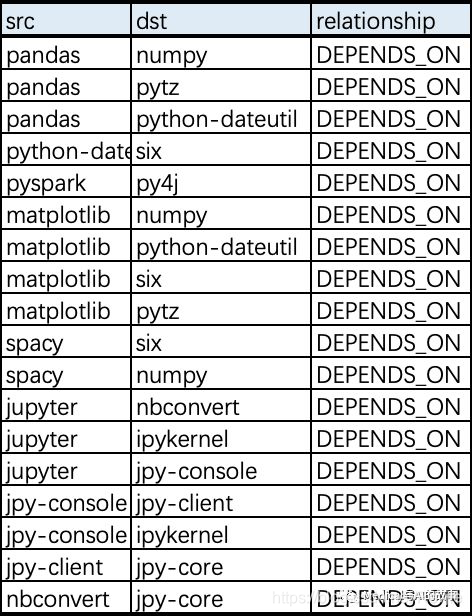依赖关系图特别适合于展示社区检测算法之间的细微的差异，因为它们往往更具关联性和层次性。尽管依赖关系图用于从软件到能源网格的各个领域，本章中的示例是针对包含Python库之间依赖关系的图运行的。开发人员使用这种软件依赖关系图来跟踪软件项目中的可传递依赖关系和冲突。你可以从书的Github存储库下载节点和文件。 表6-2 sw-nodes.csv 在这里插入图片描述 表6-3 sw-relationships.csv 在这里插入图片描述 图6-2显示了我们想要构建的图。在这个图中，我们看到所有库分成三个组（之间相互断开）。我们可以使用较小数据集上的可视化作为工具来帮助验证由社区检测算法计算出来的聚类。 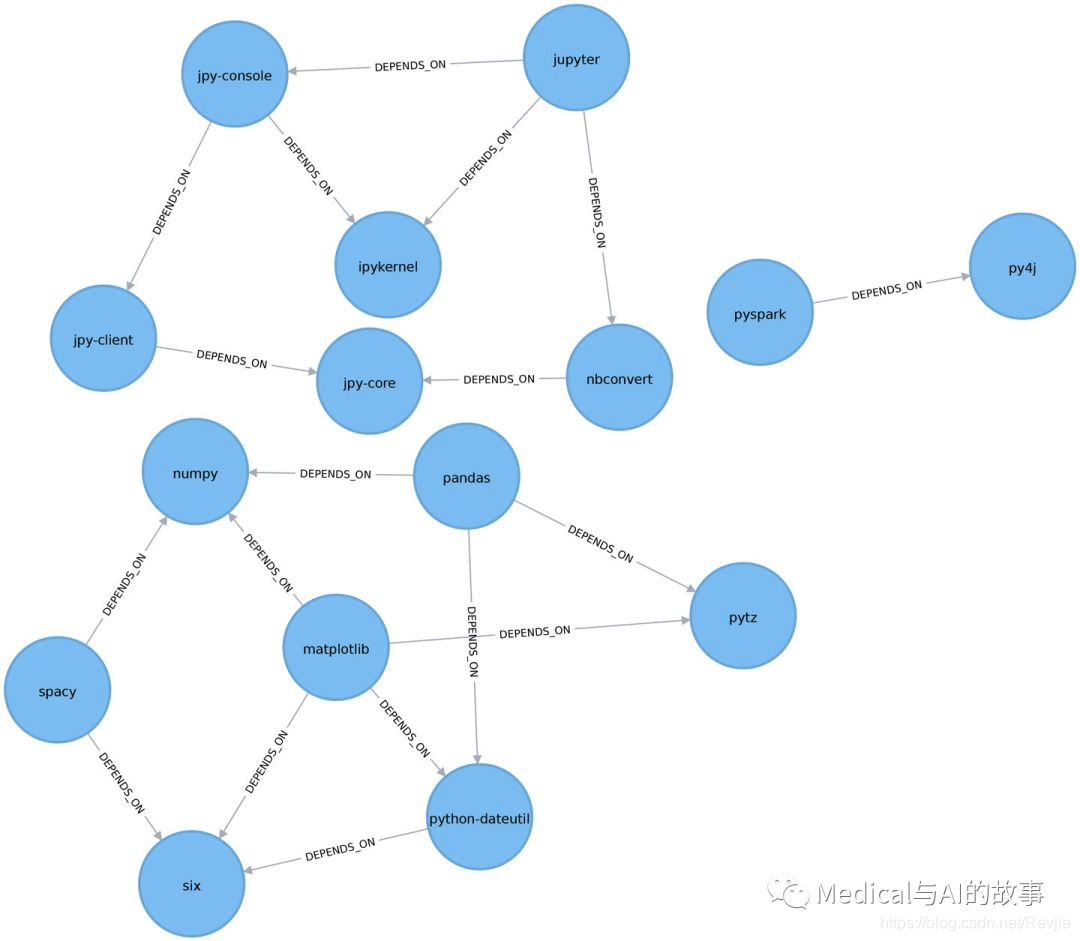在这里插入图片描述 图6-2.图模型

让我们用示例csv文件中的数据，在Spark和Neo4j中创建图。

将数据导入Apache Spark

我们将首先从Apache Spark和graphframes包中导入所需的包：

from graphframes import *

以下函数从示例csv文件创建一个GraphFrame：

def create_software_graph():
    base = "file:///home/retire2053/source/graph_algorithms_resources/"
    nodes = spark.read.csv(base+"data/sw-nodes.csv", header=True)
    relationships = spark.read.csv(base+"data/sw-relationships.csv", header=True)
    return GraphFrame(nodes, relationships)

现在来调用这个函数。

g = create_software_graph()

向Neo4j中导入数据

我们将在Neo4j中做相同的事情。这段查询将导入节点。

WITH "https://github.com/neo4j-graph-analytics/book/raw/master/data/" AS base
WITH base + "sw-nodes.csv" AS uri
LOAD CSV WITH HEADERS FROM uri AS row
MERGE (:Library {id: row.id})

以下查询将会导入关系。

WITH "https://github.com/neo4j-graph-analytics/book/raw/master/data/" AS base
WITH base + "sw-relationships.csv" AS uri
LOAD CSV WITH HEADERS FROM uri AS row
MATCH (source:Library {id: row.src})
MATCH (destination:Library {id: row.dst})
MERGE (source)-[:DEPENDS_ON]->(destination)

现在，我们已经加载了我们的图，现在可以开始算法了！

三角形计数和聚类系数

三角形计数(triangle count)算法和聚类系数(clustering coefficient)算法由于经常一起使用，因而常同时出现。三角形计数确定通过图中每个节点的三角形数。三角形是由三个节点组成的集合，三个节点中的每个节点与所有其他节点都有关系。三角形计数也可以全局运行以评估我们的整体数据集。 在这里插入图片描述 具有大量三角形的网络更有可能展现出小世界（small-world）的结构和行为。

聚类系数算法的目标是测量一个组的聚类程度（how tightly it is clustered）与它的可能的聚类度(how tightly it could be )之比值。该算法在计算中使用三角形计数，它计算现有三角形数与可能的关系的比率。最大值为1表示组内的每个节点都连接到其他节点。

聚类系数有两种类型：局部聚类和全局聚类。

局部聚类系数：一个节点的局部聚类系数是其相邻节点也之间被互相连接的可能性。这个分数的计算涉及三角形计数。

一个节点的聚类系数可以这样计算，将通过该节点的三角形数乘以2，然后将其除以组中的最大关系数（始终是该节点的度数减去1）来求得。图6-3描述了具有五个关系的节点的不同三角形和聚类系数的示例。 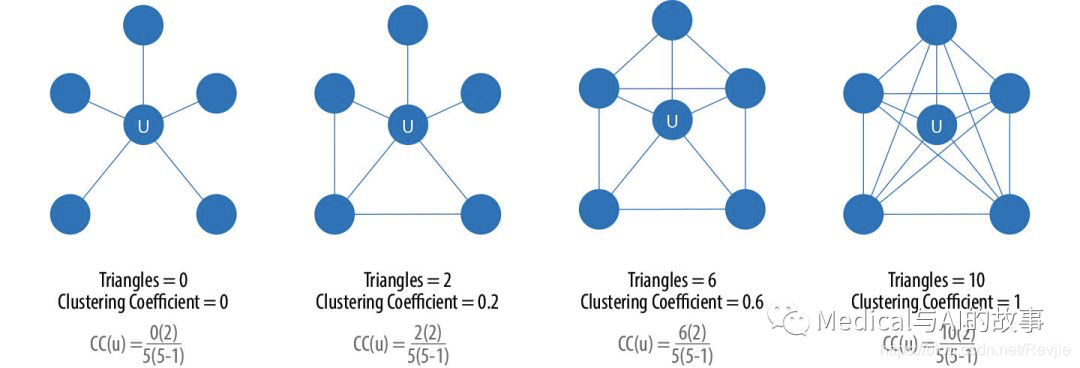在这里插入图片描述 图6-3.节点U的三角形计数和聚类系数

在图6-3中，我们使用一个具有五个关系的节点，这使得聚类系数始终等于三角形数的10%。我们可以看到，当我们改变关系的数量时，情况并非如此。如果我们把第二个例子改为有四个关系（和相同的两个三角形），那么系数是0.33。

节点的聚类系数使用以下公式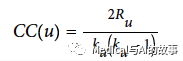： 在这里插入图片描述 在这个公式中

  • u是一个节点
  • Ru是通过u的某两个邻居的关系数（这正好就是通过u的三角形数量）。
  • Ku是u的度数

全局聚类系数：全局聚类系数是局部聚类系数的归一化之后的和。聚类系数为我们提供了一种有效的方法来寻找明显的群体，如小团体，其中每个节点都与所有其他节点有关系，但我们也可以指定阈值来设置级别（例如，节点有40%的连接）。

三角形计数和聚类系数的使用场景

当你需要确定组的稳定性（相互连接的数量，代表了稳定性）或作为其他网络度量（如聚类系数）的一部分时，请使用三角形计数。三角计数在社交网络分析中很流行，它被用来检测社区。

聚类系数可以提供随机选择的节点被连接的概率。您还可以使用它快速评估特定组或整个网络的内聚性。这些算法一起用于估计弹性和寻找网络结构。 示例用例包括：

  • 识别将给定网站分类为垃圾内容的功能。这一点在L. Becchetti等人的论文“Efficient Semi-Streaming Algorithms for Local Triangle Counting in Massive Graphs”中进行了描述。
  • 调查Facebook社交图的社区结构，研究人员在一张原本稀疏的全球图中发现了密集的用户社区。这项研究发表在J.Ugander等人的论文《The Anatomy of the Facebook Social Graph》中。
  • 探索网页的主题结构，并基于网页之间的相互链接，检测具有共同主题的网页社区。有关更多信息，请参见J. P. Eckmann和E. Moses的“Curvature of Co-Links Uncovers Hidden Thematic Layers in the World Wide Web”。

Apache Spark上的三角形计数算法

现在我们准备执行三角形计数算法。我们可以使用以下代码：

result = g.triangleCount()
(result.sort("count", ascending=False)
.filter('count > 0')
.show())

如果我们在PySpark中运行该代码，我们将看到这个输出：

+-----+---------------+
|count|             id|
+-----+---------------+
|    1|            six|
|    1|      ipykernel|
|    1|        jupyter|
|    1|python-dateutil|
|    1|     matplotlib|
|    1|    jpy-console|
+-----+---------------+

图中的三角形表示一个节点的两个邻居节点也相互之间是邻居。我们有六个库参与了这种三角关系。 如果我们想知道哪些节点在这些三角形？这就需要一个stream中包含三角形。为此，我们需要Neo4j。

Neo4j的三角形计数

使用Spark无法获取三角形的具体结果，但我们可以使用Neo4j得到这个返回值：

CALL algo.triangle.stream("Library","DEPENDS_ON")
YIELD nodeA, nodeB, nodeC
RETURN algo.getNodeById(nodeA).id AS nodeA,
algo.getNodeById(nodeB).id AS nodeB,
algo.getNodeById(nodeC).id AS nodeC

运行这个查询，可以得到如下的结果

+-----------------------------------------------------------+
| nodeA             | nodeB             | nodeC             |
+-----------------------------------------------------------+
| "six"             | "python-dateutil" | "matplotlib"      |
| "python-dateutil" | "six"             | "matplotlib"      |
| "matplotlib"      | "six"             | "python-dateutil" |
| "jupyter"         | "jpy-console"     | "ipykernel"       |
| "jpy-console"     | "jupyter"         | "ipykernel"       |
| "ipykernel"       | "jupyter"         | "jpy-console"     |
+-----------------------------------------------------------+

我们看到的六个库和之前的结果一样，但现在我们知道它们是如何连接的。matplotlib、six和python-dateutil构成一个三角形。jupyter、jpy-console和ipykernel构成另一个。

我们可以在图6-4中看到这些三角形。 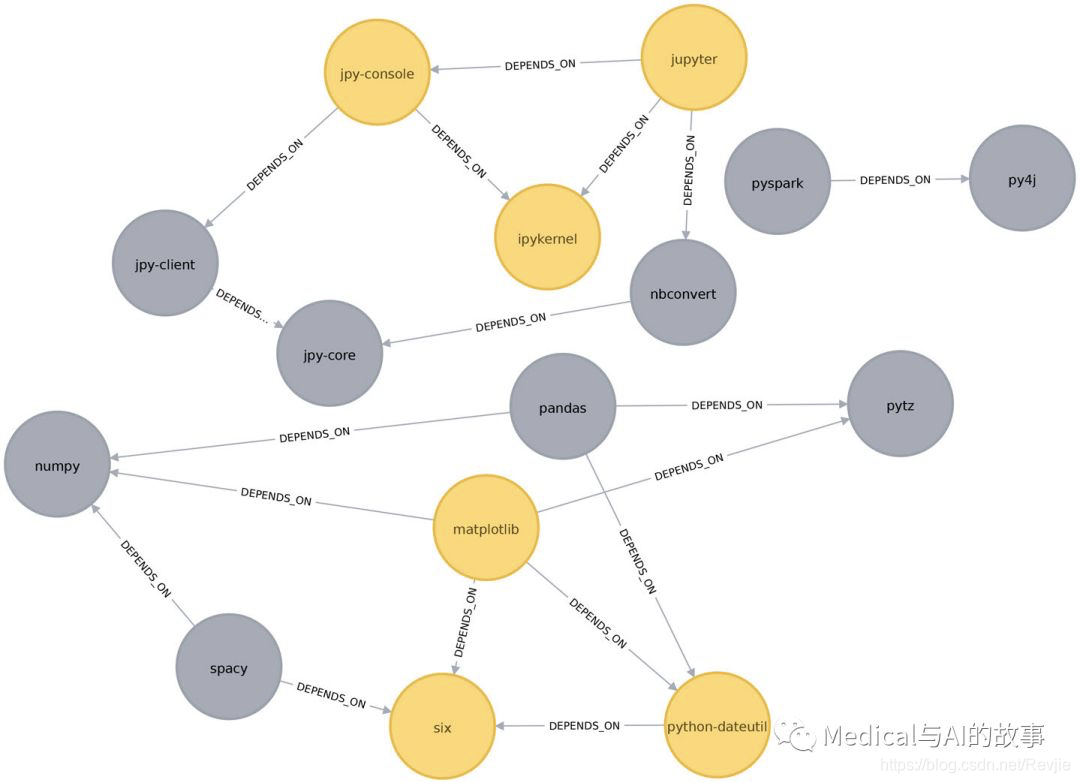在这里插入图片描述 图6-4.软件依赖关系图中的三角形

Neo4j的局部聚类系数

还可以求出局部聚类系数。以下查询将为每个节点计算此值：

CALL algo.triangleCount.stream('Library', 'DEPENDS_ON')
YIELD nodeId, triangles, coefficient
WHERE coefficient > 0
RETURN algo.getNodeById(nodeId).id AS library, coefficient
ORDER BY coefficient DESC

运行该查询，可以得到如下的结果：

+-----------------------------------------+
| library           | coefficient         |
+-----------------------------------------+
| "ipykernel"       | 1.0                 |
| "six"             | 0.3333333333333333  |
| "python-dateutil" | 0.3333333333333333  |
| "jupyter"         | 0.3333333333333333  |
| "jpy-console"     | 0.3333333333333333  |
| "matplotlib"      | 0.16666666666666666 |
+-----------------------------------------+

ipykernel的分数是1，这意味着ipykernel的所有邻居节点都是彼此的邻居。我们可以在图6-4中清楚地看到这一点。这告诉我们，直接围绕ipykernel的社区是非常有凝聚力的。

在这个代码示例中，我们过滤了系数得分为0的节点，但是系数较低的节点也可能很有趣。一个低分可以表示一个节点是一个结构孔。结构空可能是一个与其他社区中的节点连接良好的节点，而这些社区之间在其他方面没有相互连接。这是我们在第5章中讨论的一种寻找潜在桥梁的方法。

回到顶部