图算法系列《第五章中心性算法-2》 - Neo4j 图数据库中文社区

紧密中心性（Closeness Centrality）

紧密性中心性是一种检测节点通过子图传播信息有效性的方法。该方法度量是节点与所有其他节点的距离近的程度。高紧密中心性的节点与所有其他节点的距离最短。

在所有节点对的最短路径计算的基础上，紧密中心性算法，计算一个节点到所有其他节点的距离之和。然后将得到的和求倒数，以确定该节点的紧密性中心性得分。节点的紧密中心性用以下的公式来计算：在这里插入图片描述在这个公式中

u是一个节点。
n是图中的节点数。
d(u,v)是另一个节点V和U之间的最短路径距离。

更常见的是将该分数归一化，使该得分代表最短路径的平均长度，而不是它们的总和。这种调整允许比较不同大小图节点的紧密性中心性。归一化后的紧密中心性公式如下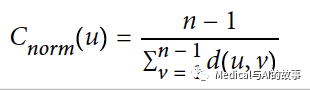：在这里插入图片描述紧密中心性算法的使用场景

当你需要知道哪个节点传播的东西最快时，应使用紧密中心性。在紧密中心性算法中，使用加权关系的话，会特别有助于评估交流和行为分析中的交互速度。示例用例包括：

发现对控制和获取组织内重要信息和资源处于非常有利位置的个人。这方面的一项研究是V. E. Krebs的“Mapping Networks of Terrorist Cells”。
作为一种启发式方法，用于估计电信和包裹交付中的到达时间，在交付过程中，内容通过最短路径流向预先定义的目标。它还被用来揭示通过所有最短路径同时传播的情况，例如通过当地社区传播的感染。在S. P. Borgatti的 “Centrality and Network Flow”中找到更多细节。
可以应用在基于基于图的关键字提取过程，比如评估文档中单词的重要性。这一过程由F. Boudin在“A Comparison of Centrality Measures for Graph-Based Keyphrase Extraction”中有描述。

紧密性中心性在连通图上效果最好。当该公式应用于一个不连通图时，两个节点之间的距离是无限的，两个节点之间没有路径。这意味着，当我们计算所有节点到那个节点的距离并求和时，我们将得到一个无限大的紧密中心性分数。在下一个示例之后将给出原始公式的变体，用来避免这种情况。

Apache Spark上的紧密中心性算法

Apache Spark没有提供一个紧密中心性的内置算法，但是我们可以用aggregateMessages框架来实现，这个框架在最短路径算法部分已经介绍过了。在我们创建函数之间，我们需要导入将会用到的包。

from graphframes.lib import AggregateMessages as AM
from pyspark.sql import functions as F
from pyspark.sql.types import *
from operator import itemgetter

我们创建几个稍后会被引用到的自定义函数（user-defined function)

def collect_paths(paths):
    return F.collect_set(paths)
collect_paths_udf = F.udf(collect_paths, ArrayType(StringType()))
paths_type = ArrayType(
    StructType([StructField("id", StringType()), StructField("distance", IntegerType())]))
def flatten(ids):
    flat_list = [item for sublist in ids for item in sublist]
    return list(dict(sorted(flat_list, key=itemgetter(0))).items())
flatten_udf = F.udf(flatten, paths_type)
def new_paths(paths, id):
    paths = [{"id": col1, "distance": col2 + 1} for col1,
    col2 in paths if col1 != id]
    paths.append({"id": id, "distance": 1})
    return paths
new_paths_udf = F.udf(new_paths, paths_type)
def merge_paths(ids, new_ids, id):
    joined_ids = ids + (new_ids if new_ids else [])
    merged_ids = [(col1, col2) for col1, col2 in joined_ids if col1 != id]
    best_ids = dict(sorted(merged_ids, key=itemgetter(1), reverse=True))
    return [{"id": col1, "distance": col2} for col1, col2 in best_ids.items()]
merge_paths_udf = F.udf(merge_paths, paths_type)
def calculate_closeness(ids):
    nodes = len(ids)
    total_distance = sum([col2 for col1, col2 in ids])
    return 0 if total_distance == 0 else nodes * 1.0 / total_distance
    closeness_udf = F.udf(calculate_closeness, DoubleType())
closeness_udf = F.udf(calculate_closeness, DoubleType())

以下代码是计算每个节点的紧密中心性

vertices = g.vertices.withColumn("ids", F.array())
cached_vertices = AM.getCachedDataFrame(vertices)
g2 = GraphFrame(cached_vertices, g.edges)
for i in range(0, g2.vertices.count()):
    msg_dst = new_paths_udf(AM.src["ids"], AM.src["id"])
    msg_src = new_paths_udf(AM.dst["ids"], AM.dst["id"])
    agg = g2.aggregateMessages(F.collect_set(AM.msg).alias("agg"),
                sendToSrc=msg_src, sendToDst=msg_dst)
    res = agg.withColumn("newIds", flatten_udf("agg")).drop("agg")
    new_vertices = (g2.vertices.join(res, on="id", how="left_outer")
            .withColumn("mergedIds", merge_paths_udf("ids", "newIds",
            "id")).drop("ids", "newIds")
            .withColumnRenamed("mergedIds", "ids"))
    cached_new_vertices = AM.getCachedDataFrame(new_vertices)
    g2 = GraphFrame(cached_new_vertices, g2.edges)
(g2.vertices
.withColumn("closeness", closeness_udf("ids"))
.sort("closeness", ascending=False)
.show(truncate=False))

结果如下。Alice、Doug和David是图中连接最紧密的节点，得分为1.0，这意味着每个节点都直接连接到图中其部分的所有节点。

+-------+-----------------------------------------------------------------+------------------+
|id     |ids                                                              |closeness         |
+-------+-----------------------------------------------------------------+------------------+
|Alice  |[[Bridget, 1], [Doug, 1], [Charles, 1], [Michael, 1], [Mark, 1]] |1.0               |
|Doug   |[[Bridget, 1], [Charles, 1], [Michael, 1], [Mark, 1], [Alice, 1]]|1.0               |
|David  |[[James, 1], [Amy, 1]]                                           |1.0               |
|Bridget|[[Doug, 1], [Charles, 2], [Michael, 1], [Mark, 2], [Alice, 1]]   |0.7142857142857143|
|Michael|[[Bridget, 1], [Doug, 1], [Charles, 2], [Mark, 2], [Alice, 1]]   |0.7142857142857143|
|James  |[[David, 1], [Amy, 2]]                                           |0.6666666666666666|
|Amy    |[[James, 2], [David, 1]]                                         |0.6666666666666666|
|Charles|[[Bridget, 2], [Doug, 1], [Michael, 2], [Mark, 2], [Alice, 1]]   |0.625             |
|Mark   |[[Bridget, 2], [Doug, 1], [Charles, 2], [Michael, 2], [Alice, 1]]|0.625             |
+-------+-----------------------------------------------------------------+------------------+

图5-5说明了即使David在密友群中只有几个联系，但他在他的群体中，也是重要的。换句话说，这个分数表示每个用户在其子图（能连通的到的子图）中与其他用户之间的亲密程度，而不一定全图。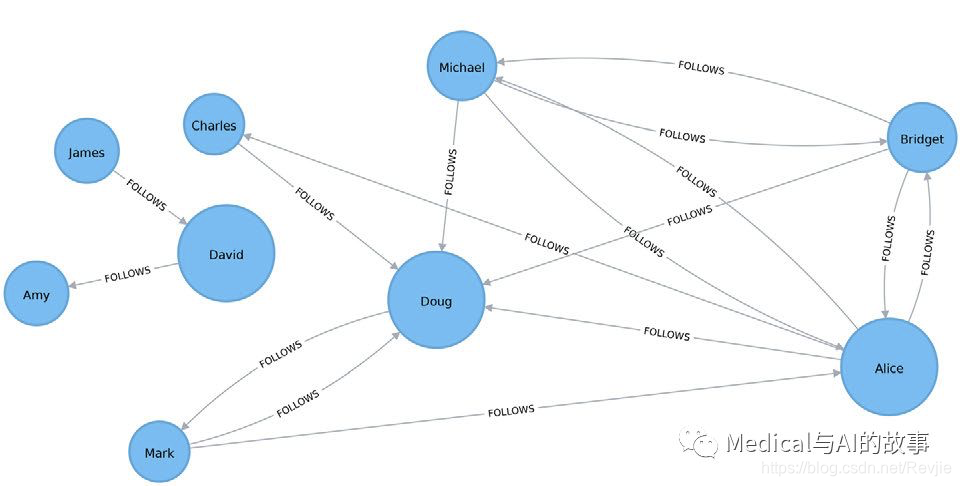在这里插入图片描述图5-5.紧密中心性的可视化

Neo4j上的紧密中心性

Neo4j上用如下的公式来实现紧密中心性算法。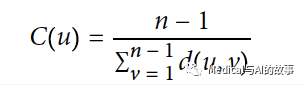在这里插入图片描述在这个公式中，

u是一个节点
n是在当前组件（component）内节点数量
d(u,v)是其他节点v和u之间的最短路径。运行如下查询，将会计算图中每个节点的紧密中心性。

CALL algo.closeness.stream("User", "FOLLOWS")
YIELD nodeId, centrality
RETURN algo.getNodeById(nodeId).id, centrality
ORDER BY centrality DESC

以下是运行的结果

+--------------------------------------------------+
| algo.getNodeById(nodeId).id | centrality         |
+--------------------------------------------------+
| "Alice"                     | 1.0                |
| "Doug"                      | 1.0                |
| "David"                     | 1.0                |
| "Bridget"                   | 0.7142857142857143 |
| "Michael"                   | 0.7142857142857143 |
| "Amy"                       | 0.6666666666666666 |
| "James"                     | 0.6666666666666666 |
| "Charles"                   | 0.625              |
| "Mark"                      | 0.625              |
+--------------------------------------------------+

我们得到了与Spark算法相同的结果，但是，和以前一样，分数代表了他们在子图中与其他人的紧密程度，而不是整个图。在这里插入图片描述在严格意义上的紧密性中心性算法中，我们图中的所有节点都会得到无穷大的分数，因为每个节点至少有一个它无法到达的其他节点。不过，实现每个断开的组件（component，局部连通的图）的得分通常会更有用。

理想情况下，我们希望在整个图中得到一个中心性的整体认识，在接下来的两个部分中，我们将学习实现紧密中心性算法的一些变体，它们将实现这一点。

紧密中心性的变体：Wasserman & Faust

Stanley Wasserman和Katherine Faust提出了一个改进的公式，用于计算具有多个无相互连接的子图的紧密中心性。他们的书Social Network Analysis: Methods and Applications中详细介绍了他们的公式。此公式的结果是可到达组中节点的分数与可到达节点的平均距离之比。公式如下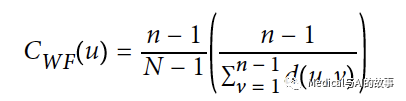：在这里插入图片描述在这个公式中

u是一个节点
N是所有节点的数量
n是u所在的组件上的节点数量
d(u,v)是在其他节点v和u之间的最短路径

为了能够使用这个公式，我们可以通过传递参数{improved:true}给紧密中心性算法。

以下查询使用Wasserman & Faust紧密中心性算法：

CALL algo.closeness.stream("User", "FOLLOWS", {improved: true})
YIELD nodeId, centrality
RETURN algo.getNodeById(nodeId).id AS user, centrality
ORDER BY centrality DESC

运行的结果如下：

+---------------------------------+
| user      | centrality          |
+---------------------------------+
| "Alice"   | 0.5                 |
| "Doug"    | 0.5                 |
| "Bridget" | 0.35714285714285715 |
| "Michael" | 0.35714285714285715 |
| "Charles" | 0.3125              |
| "Mark"    | 0.3125              |
| "David"   | 0.125               |
| "Amy"     | 0.08333333333333333 |
| "James"   | 0.08333333333333333 |
+---------------------------------+

如图5-6所示，结果现在更能代表节点与整个图的紧密性。较小子图（David、Amy和James）成员的得分已被降低，现在他们的得分是所有用户中最低的。这很有意义，因为它们是最孤立的节点。这个公式对于检测节点在整个图中的重要性更有用，而不是在它自己的子图中。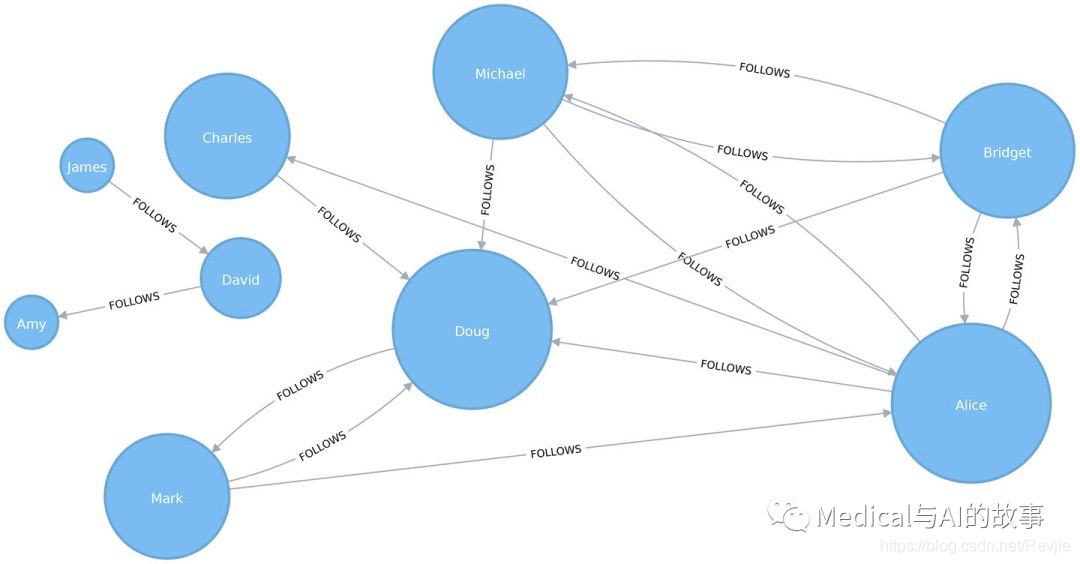在这里插入图片描述图5-6.紧密性中心性的可视化在下一节中，我们将学习和谐中心性算法，它使用另一个公式来计算紧密性，从而获得类似的结果。

紧密中心性变体：和谐中心性和谐中心性（也称为值化中心性）是紧密中心性的一种变体，被发明来解决不连通图的问题。在《Harmony in a Small World》一书中，M. Marchiori和 V. Latora提出了这个概念，作为一个平均最短路径的实用表示。在计算每个节点的接近度得分时，它不是求一个节点到所有其他节点的距离之和，而是求这些距离的倒数。这意味着无穷大的值变得无关紧要。基础的和谐中心性算法使用以下公式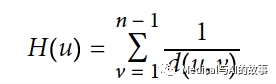：在这里插入图片描述在公式中

u是一个节点
n是图中的节点数
d(u,v)是在其他节点v和u之间的最短路径

与紧密中心性一样，我们也可以用以下公式计算归一化和谐中心性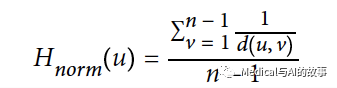：在这里插入图片描述在这个共识中，无穷大被很干净利索地处理掉了。

Neo4j上的和谐中心性

用如下的查询来执行和谐中心性算法。

CALL algo.closeness.harmonic.stream("User", "FOLLOWS")
YIELD nodeId, centrality
RETURN algo.getNodeById(nodeId).id AS user, centrality
ORDER BY centrality DESC

该Procedure的运行结果如下：

+------------------------+
| user      | centrality |
+------------------------+
| "Alice"   | 0.625      |
| "Doug"    | 0.625      |
| "Bridget" | 0.5        |
| "Michael" | 0.5        |
| "Charles" | 0.4375     |
| "Mark"    | 0.4375     |
| "David"   | 0.25       |
| "Amy"     | 0.1875     |
| "James"   | 0.1875     |
+------------------------+

该算法的结果与原始的紧密性中心性算法不同，但与Wasserman和Faust改进算法的结果相似。当处理具有多个连接组件的图时，可以使用任一算法。

中介中心性（Betweenness Centrality）

有时，系统中最重要的齿轮不是最明显的动力最高的齿轮。有时反而是一些中间环节把对资源或信息流控制最大的群体或经纪人联系起来。中介中心性是一种检测节点对图中信息或资源流的影响程度的方法。它通常用于查找充当从图的一部分到另一部分的桥梁型节点。

中介中心性算法首先计算连接图中每对节点之间的最短（权重）路径。每个节点都会根据这些通过该节点的最短路径的数量得到一个分数。经过节点的最短路径越多，该节点的得分越高。

当Linton C. Freeman在1971年的论文A Set of Measures of Centrality Based on Betweenness中介绍这个概念后，中介中心性被认为是“三个截然不同的直观的中心性概念”之一。

桥和控制点

网络中的桥可以是节点或关系。在一个非常简单的图中，您可以通过查找节点或关系来找到它们，如果删除这些节点或关系，将导致图的一部分断开连接。然而，由于这种简单情形在典型的图并不是实际发生，实际情况会更复杂，我们需要使用中介中心性算法来评估在一个群体中某个节点的中介特性。

如果一个节点位于这些节点之间的每一条最短路径上，则它被认为是其他两个节点的关键，如图5-7所示。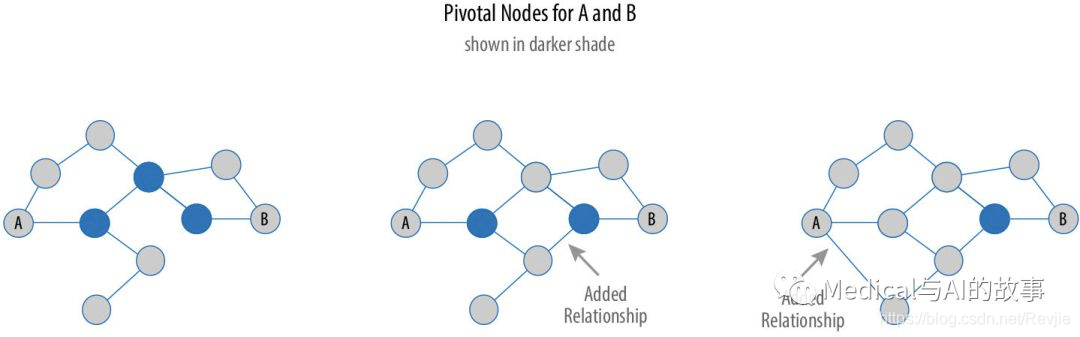在这里插入图片描述图5-7.关键节点位于两个节点之间的每一条最短路径上。所以，创建更多的最短路径，会减少这个关键节点的数量，并减少风险。

关键节点（pivotal node）在连接其他节点时起着重要作用。如果删除关键节点，则各节点对的新的最短路径将更长或更昂贵。这可以作为评估单一脆弱性点的考虑因素。

计算中介中心性

中介中心性是将最短路径通过如下公式计算后累加的结果。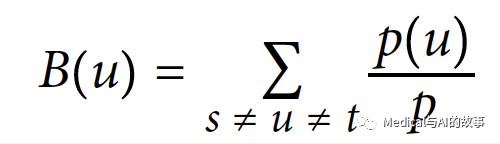在这里插入图片描述在公式中

u是一个节点
p是节点s和t之间最短路径的数量
p(u)是s和t之间通过u的最短路径的数量图5-8显示了计算出中介中心性的步骤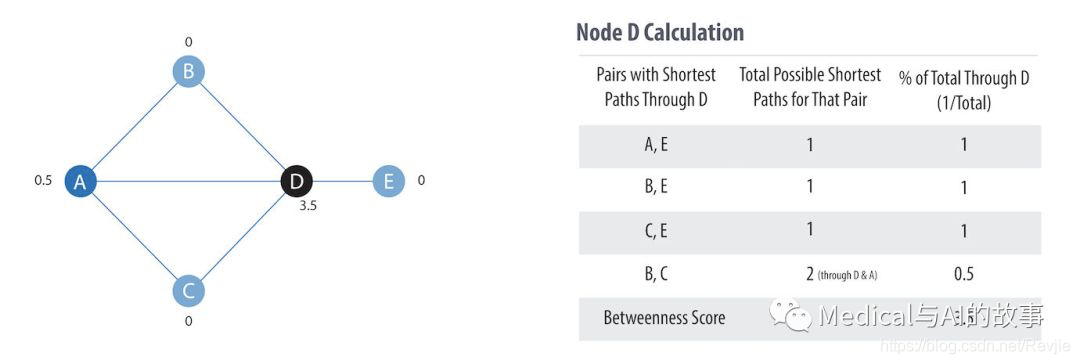图5-8. 计算中介中心性的基本概念

这是计算过程：

对于每个节点，找到通过它的所有最短路径。 B、C、E没有最短路径，并被赋值为0。
对于步骤1中的每个最短路径，计算其在该对可能最短路径总数中的百分比。（两点间可能有多条最短路径）
将步骤2中的所有值相加，以找到节点的中间中心性得分。图5-8中的表说明了节点D的步骤2和3。
对每个节点重复该过程。

中介中心性算法的使用场景

中介中心性适用于现实网络中的各种问题。我们使用它来发现瓶颈、控制点和漏洞。示例用例包括：

识别不同组织中的影响因素。有权势的个人不一定在管理岗位上，但可以出现在“中介性岗位”上，这能够通过中介中心性来找到。消除这些影响者会严重破坏组织的稳定。如果该组织是犯罪组织，这可能被认为是一种很有效的执法方式；另一种场景下，但是如果企业失去了被低估的关键员工，这可能是一场灾难。更多细节见C. Morselli和J. Roy的Brokerage Qualifications in Ringing Operations。
发现电网等网络中的关键转移点。与直觉相反，移除特定的桥梁或者关键节点，实际上可以通过使得干扰因素孤岛化而提高整体的鲁棒性。研究细节包含在R. Sol.等人的“Robustness of the European Power Grids Under Intentional Attack”中。
通过为目标人物提供推荐引擎，帮助微博用户在Twitter上传播他们的影响力。这一方法在S. Wu等人的一篇论文“Making Recommendations in a Microblog to Improve the Impact of a Focal User”中进行了描述。

在这里插入图片描述中介中心性假设节点之间的所有通信都是沿着最短路径以相同的概率进行的，这在现实生活中情况并不相同。因此，它并没有给我们一个在全图中最有影响力的节点的概览，而只是提供了一个很好的表示方法。 Mark Newman在《Networks: An Introduction 》(Oxford University Press, p186)中有介绍。

Neo4j上的中介中心性

Spark没有中介中心性的内置算法，因此我们将使用Neo4j来演示此算法。调用以下过程将计算图中每个节点的中介中心性：

CALL algo.betweenness.stream("User", "FOLLOWS")
YIELD nodeId, centrality
RETURN algo.getNodeById(nodeId).id AS user, centrality
ORDER BY centrality DESC

运行这个procedure可以得到如下的结果：

+------------------------+
| user      | centrality |
+------------------------+
| "Alice"   | 10.0       |
| "Doug"    | 7.0        |
| "Mark"    | 7.0        |
| "David"   | 1.0        |
| "Bridget" | 0.0        |
| "Charles" | 0.0        |
| "Michael" | 0.0        |
| "Amy"     | 0.0        |
| "James"   | 0.0        |
+------------------------+

如图5-9所示，Alice是这个网络的主要中介节点，但Mark和Doug并不落后。在较小的子图中，所有最短的路径都经过David，因此他对于这些节点之间的信息流很重要。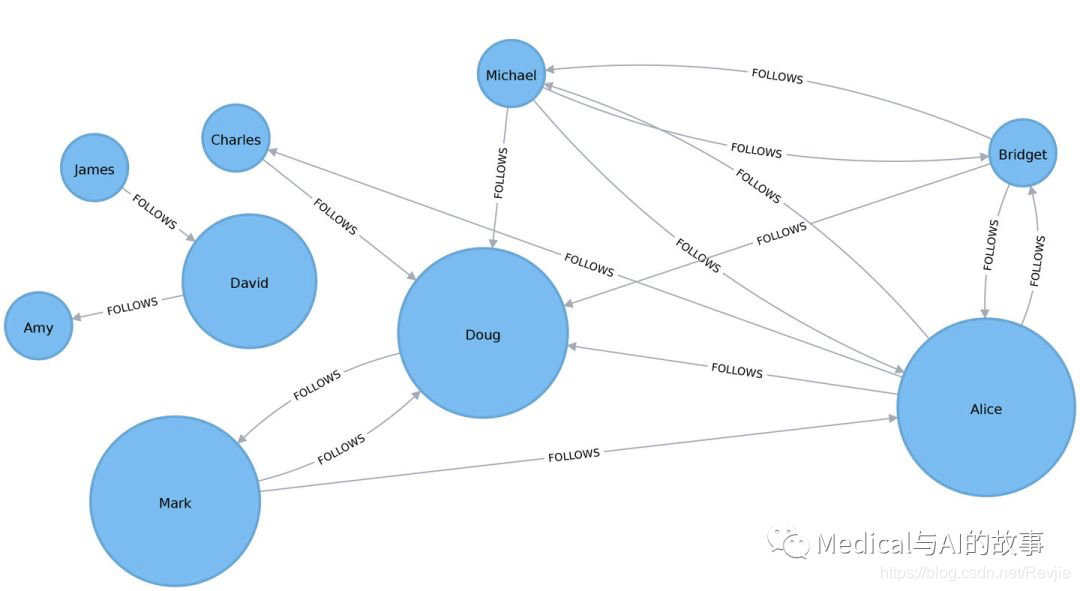在这里插入图片描述图5-9.中介中心性的可视化

在这里插入图片描述对于更大的图来说，精确的中心性计算是不实际的，因为已知最快的精确计算所有节点中间数的算法的运行时间与节点数和关系数的乘积成正比。我们可能希望先过滤后留下子图，并使用子图来（在下一节中描述）处理所有节点的子集。

我们可以将两个断开连接的图组件连接在一起，方法是引入一个名为Jason的新用户，该用户关注两个组件的用户人员，而且被两个组件的人所关注。

WITH ["James", "Michael", "Alice", "Doug", "Amy"] AS existingUsers
MATCH (existing:User) WHERE existing.id IN existingUsers
MERGE (newUser:User {id: "Jason"})
MERGE (newUser)<-[:FOLLOWS]-(existing)
MERGE (newUser)-[:FOLLOWS]->(existing)

如果我们重新运行算法，我们将看到这个输出：

+--------------------------------+
| user      | centrality         |
+--------------------------------+
| "Jason"   | 44.33333333333333  |
| "Doug"    | 18.333333333333332 |
| "Alice"   | 16.666666666666664 |
| "Amy"     | 8.0                |
| "James"   | 8.0                |
| "Michael" | 4.0                |
| "Mark"    | 2.1666666666666665 |
| "David"   | 0.5                |
| "Bridget" | 0.0                |
| "Charles" | 0.0                |
+--------------------------------+

Jason的得分最高，因为这两组用户之间的交流将通过他。可以说Jason是两组用户之间的本地桥梁，如图5-10所示。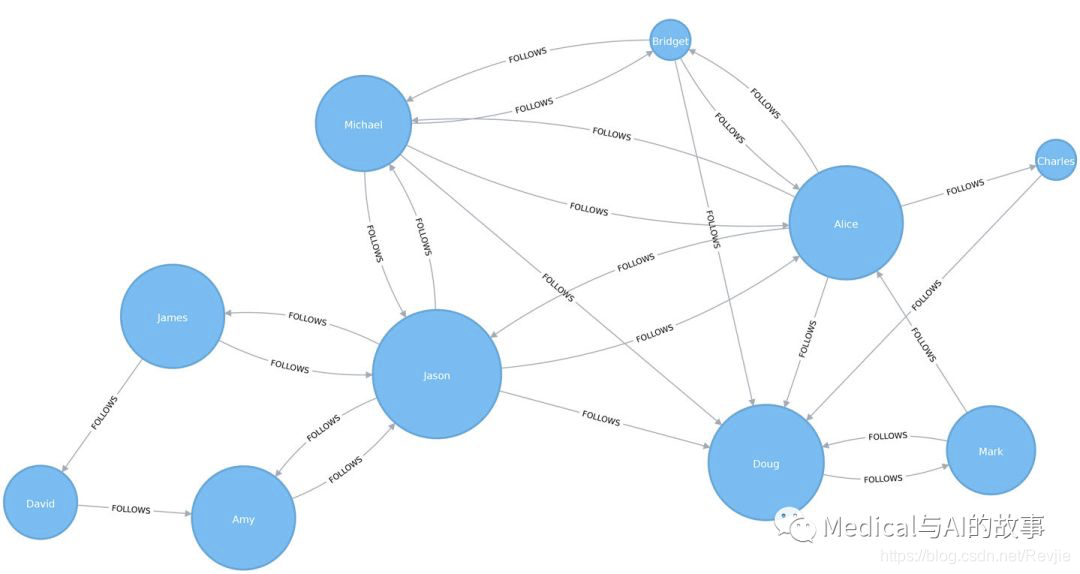在这里插入图片描述在我们继续下一节之前，让我们通过删除Jason和他的关系：

MATCH (user:User {id: "Jason"}) DETACH DELETE user