中介中心性变体：RA-Brandes

回想一下，在大规模图上计算精确的中介中心性是非常昂贵的。因此，我们可以选择使用运行速度更快但仍然提供有用信息（尽管不精确）的近似算法。

Randomized-Approximate Brandes（随机近似 Brandes，简称RA-Brandes）算法是计算中介中心性近似分数的最著名算法。RA-Brandes算法不计算每对节点之间的最短路径，只考虑所有节点的一个子集。而选择节点的子集的两种常见策略是分别是：

• 随机（random）策略：节点的选择是一致的，随机的，具有确定的选择概率。默认概率为：lgN/(e^2)。如果概率是1，意味着所有的节点都被装载，这样RA-Brandes算法和通常的中介中心性是一致的。
• 度（degree）策略：节点是随机选择的，但是那些度低于平均值的节点会被自动排除（即只有具有大量关系的节点才有机会被访问）。 作为进一步的优化，您可以限制最短路径算法使用的深度，这样该算法将会提供所有最短路径的子集。

用Neo4j实现RA-Brandes

用查询来执行随机模式下的RA-Brandes算法：

CALL algo.betweenness.sampled.stream("User", "FOLLOWS", {strategy:"degree"})
YIELD nodeId, centrality
RETURN algo.getNodeById(nodeId).id AS user, centrality
ORDER BY centrality DESC

这将会得到如下的结果：

+------------------------+
| user      | centrality |
+------------------------+
| "Alice"   | 9.0        |
| "Mark"    | 9.0        |
| "Doug"    | 4.5        |
| "David"   | 2.25       |
| "Bridget" | 0.0        |
| "Charles" | 0.0        |
| "Michael" | 0.0        |
| "Amy"     | 0.0        |
| "James"   | 0.0        |
+------------------------+

尽管Mark现在的排名比Doug高，我们最有影响力的人和以前差不多。由于此算法的随机性，每次运行它时，我们可能会看到不同的结果。相比于小样本图，在较大的图上，这种随机性的影响要小一些。

页面排名(PageRank)

网页排名（PageRank）是最著名的中心性算法。它测量节点的传递（或方向）影响。我们讨论的所有其他中心性算法都度量节点的直接影响，而网页排名算法则考虑节点的邻居及其邻居的影响。例如，拥有一些非常强大的朋友比拥有很多不那么强大的朋友能让你更有影响力。网页排名算法可以通过迭代地将一个节点的排名分布在其相邻节点上，或者通过随机遍历图并计算在这些遍历过程中每个节点的命中频率来计算。

PageRank是以谷歌创始人之一Larry Page的名字命名的，Larry Page创建这个网站是为了在谷歌的搜索结果中对网站进行排名。其基本假设是，一个有更多传入链接和更具影响力的传入链接的页面更有可能是可靠的来源。PageRank衡量一个节点的传入关系的数量和质量，以确定该节点的重要性。对网络影响更大的节点被认为具有更多来自其他影响节点的传入关系。

影响

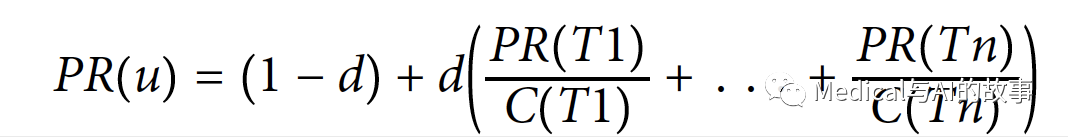在直觉上，对于“影响”(influence)是这样定义的：与不太重要节点的连接相比，与更重要节点的关系对相关节点的影响贡献更大。测量“影响”通常涉及到对节点进行评分，而节点通常连着带权重关系，这些关系在许多迭代中不断更新评分。在一些情况中，所有节点会被评分，在另外的一些情形中，通过随机产生的代表性分布上被评分。 请记住，中心性是一个节点与其他节点相比时候的重要性。中心性是对节点潜在影响的排名，而不是衡量实际的影响。例如，您可以确定两个人在一个网络中具有最高的中心性，但也许因为政策或文化规范也在发挥作用，实际上的影响力被转移到其他人。量化实际影响是制定其他的影响评估指标的一个活跃研究领域，但并不在本书的范围之内。 PageRank公式 PageRank在谷歌的论文中是这样定义的：

• 我们假设一个页面u引用了T1到Tn这n个页面。
• d是一个阻尼系数，设置在0和1之间。通常设置为0.85。您可以将这个值- 视为用户继续单击的可能性。（这有助于最小化Rank Sink，这将在下一节中解释。）
• 1-d是用户不通过任何关系而直接到达节点的概率。
• C(Tn)定义节点T的对外的度。 图5-11给出了一个小例子，说明PageRank将如何继续更新节点的评分，直到它收敛或满足所设置的迭代次数。 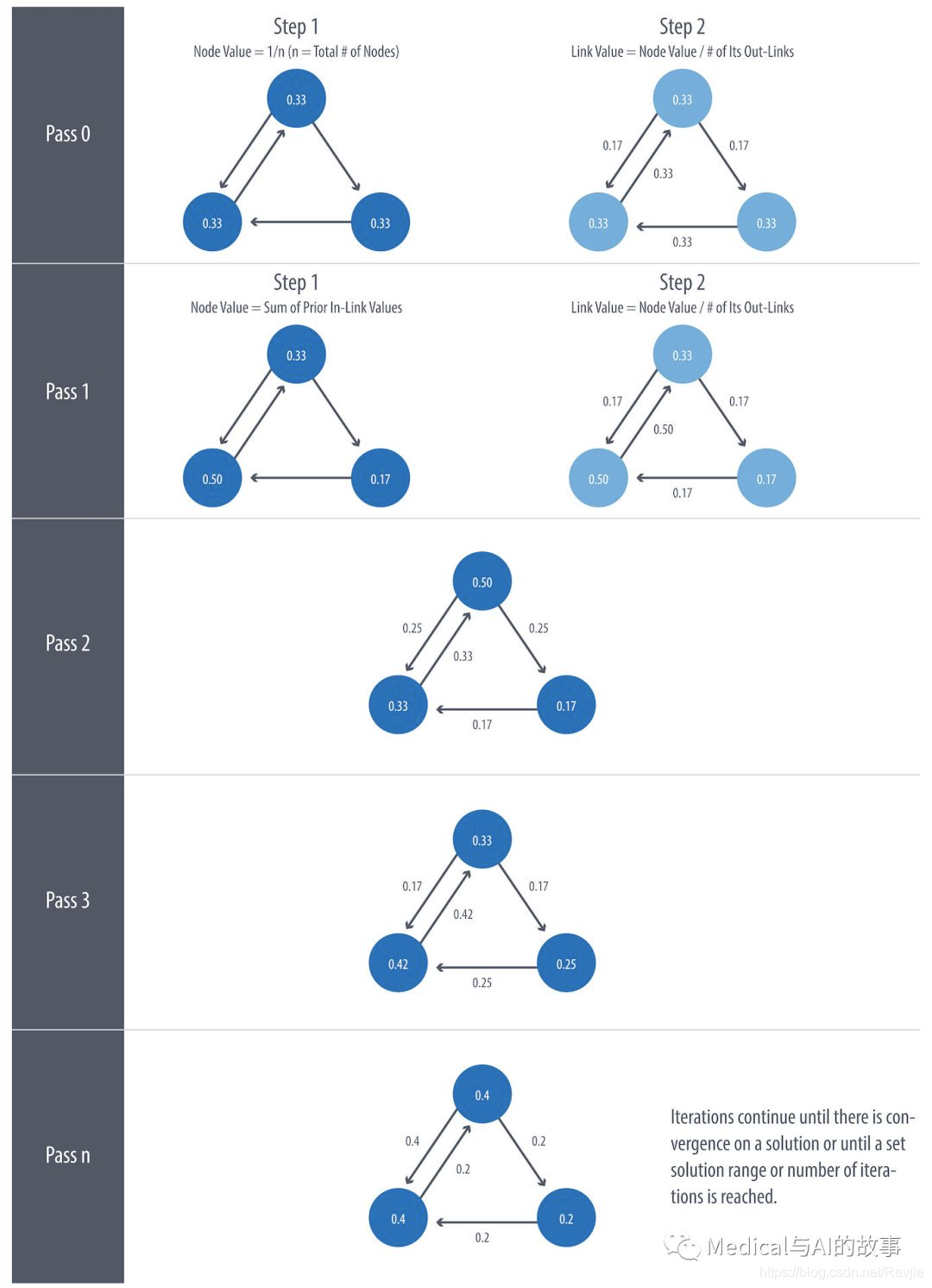图5-11.PageRank的每次迭代都有两个计算步骤：一个用于更新节点值，另一个用于更新链接值。

迭代、Random Surfers和Rank Sinks

PageRank是一种迭代算法，运行到评分收敛或达到一组迭代次数为止。从概念上讲，PageRank假设有一个网络冲浪者（web surfer）通过链接或者使用随机的URL来访问网页。阻尼系数（damping factor）d 是指下一次点击链接的概率。你可以把它看作是一个冲浪者可能会变得无聊，然后随机切换到另一个页面。PageRank分数表示通过传入链接而非随机访问页面的可能性。 没有传出关系的节点或节点组（也称为悬空节点, Dangling node），这些节点可以通过拒绝和其他节点连接，来独占PageRank分数。这就是所谓的Rank Sink。你可以把这想象成一个冲浪者被困在一个页面或页面的一个子集上，没有出路。另一个困难是节点只指向一个组中的其他节点（比如类似小世界网络的情况）。当冲浪者在节点之间来回跳跃时，循环引用会导致其等级增加。这些情况如图5-12所示。

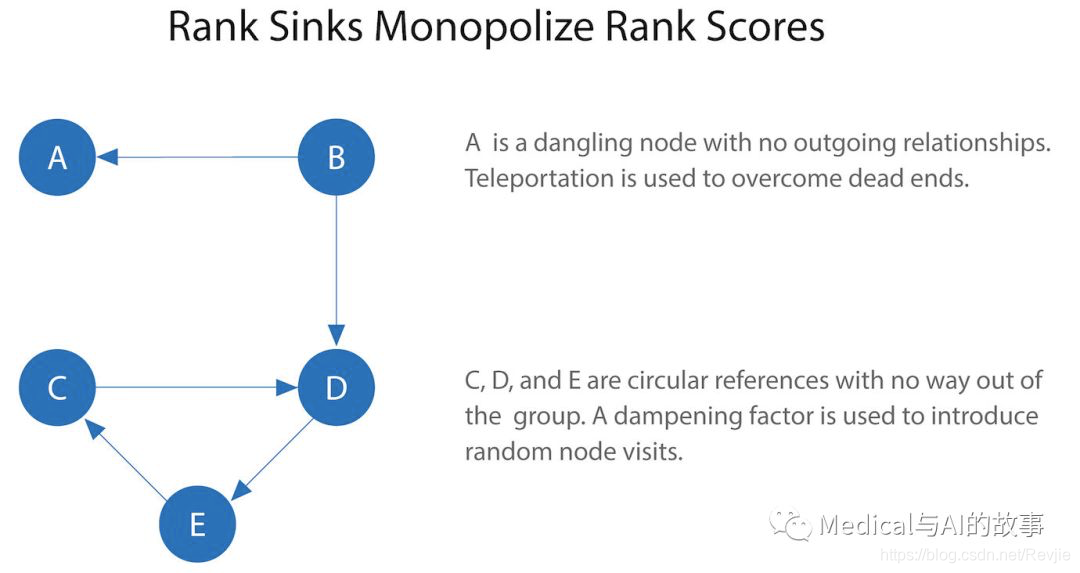
图5-12.Rank Sink是由没有传出关系的节点或节点组引起的。 有两种策略可以避免Rank Sink。首先，当到达没有传出关系的节点时，PageRank假定它对所有节点有传出关系。穿越这些看不见的链接有时被称为心灵传送（teleportation）。第二，阻尼系数（damping factor）提供了另一个避免Rank Sink的机会，通过引入直接链接与随机节点访问的概率。当您将d设置为0.85时，会有15%的可能性访问完全随机的节点。

虽然最初的公式建议的阻尼系数为0.85，但它最初的用途是在符合链接的幂律法则（大多数页面链接很少，少数页面有很多）的万维网上。降低阻尼系数会降低在进行随机跳跃之前遵循长的关系路径的可能性。反过来，这会增加节点的前置节点对其分数和排名的贡献。

如果您看到PageRank的意外结果，那么值得对该图进行一些探索性分析，以确定这些问题中是否有任何一个是原因。阅读Ian Rogers的文章“The Google PageRank Algorithm and How It Works”，了解更多信息。

PageRank算法的使用场景？

PageRank现在用于Web索引之外的许多域。只要你想在网络上获得广泛影响的计算，就使用这个算法。例如，如果你想寻找一个对生物功能影响最大的基因，它可能不是最相关的算法。事实上，这种影响最大的基因可能是和其他基因其他功能连接最多的那些基因（更多考虑度中心性）。 示例用例包括：

• 向用户提供他们可能希望关注的其他帐户的建议（Twitter为此使用个性化的PageRank）。该算法运行在一个包含共享兴趣和公共的连接的图上。该方法在P. Gupta等人的论文“WTF: The Who to Follow Service at Twitter”中有更详细的描述。
• 预测公共空间或街道的交通流量和人员流动。该算法运行在道路交叉口的图上，其中PageRank分数反映了人们在每条街道上停车或结束行程的趋势。这一点在B. Jiang、S. Zhao和J. Yin的论文“Self-Organized Natural Roads for Predicting Traffic Flow: A Sensitivity Study”中有更详细的描述。
• 作为医疗和保险行业异常和欺诈检测系统的一部分。PageRank有助于揭示医生或服务提供者的异常行为，然后将分数输入机器学习算法。David Gleich在他的论文“PageRank Beyond the Web”中描述了该算法的更多用途。

Apache Spark上的网页排名算法

现在我们准备好执行PageRank算法了。GraphFrames支持PageRank的两种实现：

• 第一个实现，以固定的迭代次数运行PageRank。这可以通过设置maxIter参数来运行。
• 第二个实现，运行PageRank直到收敛。这可以通过设置tol参数来运行。

具有固定迭代次数的PageRank

让我们看一个固定迭代的案例

results = g.pageRank(resetProbability=0.15, maxIter=20)
results.vertices.sort("pagerank", ascending=False).show()

请注意，在Spark中，阻尼系数(damping factor)更直观地称为重置概率（reset probability），其值为相反的值。也就是说，本例中的重置概率=0.15等于阻尼因子：Neo4j中的0.85。 如果我们在PySpark中运行代码，就可以看到如下的输出：

+-------+-------------------+
|     id|           pagerank|
+-------+-------------------+
|   Doug| 2.2865372087512252|
|   Mark| 2.1424484186137263|
|  Alice|  1.520330830262095|
|Michael| 0.7274429252585624|
|Bridget| 0.7274429252585624|
|Charles| 0.5213852310709753|
|    Amy| 0.5097143486157744|
|  David|0.36655842368870073|
|  James| 0.1981396884803788|
+-------+-------------------+

正如我们所料，Doug拥有最高的PageRank，因为他的子图中被所有的人所关注。虽然Mark只有一个追随者，但那个追随者是Doug，所以Mark在这个图中也被认为是重要的。重要的不仅是追随者的数量，还有这些追随者的重要性。 在PageRank算法中，图中的关系没有权重，因此每个关系都被认为是相等的。通过在关系DataFrame中指定权重列来添加关系权重。

收敛型PageRank

现在，我们将尝试运行PageRank的收敛型实现，在这个算法中，运行直到在设置的范围之内：

results = g.pageRank(resetProbability=0.15, tol=0.01)
results.vertices.sort("pagerank", ascending=False).show()

如果我们在PySpark上运行，会看到如下的结果

+-------+-------------------+
|     id|           pagerank|
+-------+-------------------+
|   Doug| 2.2233188859989745|
|   Mark|  2.090451188336932|
|  Alice| 1.5056291439101062|
|Michael|  0.733738785109624|
|Bridget|  0.733738785109624|
|    Amy|  0.559446807245026|
|Charles| 0.5338811076334145|
|  David|0.40232326274180685|
|  James|0.21747203391449021|
+-------+-------------------+

每个人的PageRank得分与固定迭代次数的变量略有不同，但正如我们所期望的，最后的排名的顺序保持不变。 尽管完美解决方案的收敛听起来很理想，但在某些情况下PageRank无法在数学意义上收敛。对于较大的图，PageRank执行时间可能很长。误差限制（tolerance limit）有助于为收敛结果设置可接受的范围，但许多人选择使用最大迭代型PageRank或者将最大迭代与收敛进行联合使用。最大迭代型PageRank通常会在性能上更稳定一些。无论您选择哪个选项，您可能需要测试几个不同的限制，以找到适合您的数据集的内容。较大的图通常需要比中等大小的图更多的迭代或更小的公差，以获得更好的精度。

Neo4j上的PageRank

我们也可以在Neo4j中运行PageRank。用以下查询来计算每个节点的PageRank：

CALL algo.pageRank.stream('User', 'FOLLOWS', {iterations:20, dampingFactor:0.85})
YIELD nodeId, score
RETURN algo.getNodeById(nodeId).id AS page, score
ORDER BY score DESC

运行该procedure将会得到如下的结果：

+---------------------------------+
| page      | score               |
+---------------------------------+
| "Doug"    | 1.671956494869664   |
| "Mark"    | 1.5623059164267037  |
| "Alice"   | 1.1116563910618424  |
| "Bridget" | 0.5358271526871249  |
| "Michael" | 0.5358271526871249  |
| "Amy"     | 0.3858750030398369  |
| "Charles" | 0.38475333093665537 |
| "David"   | 0.27750000506639483 |
| "James"   | 0.15000000000000002 |
+---------------------------------+

与Spark示例一样，Doug是最有影响力的用户，Mark紧随其后，是Doug关注的唯一用户。我们可以在图5-13中看到节点相对彼此的重要性。

PageRank有多种不同的实现，因此即使顺序相同，它们也可以产生不同的得分。Neo4j使用1减去阻尼系数来初始化节点，而SPARK使用值1。在这种情况下，最终的相对排名是相同的，但用于达到这些结果的基础得分值是不同的。 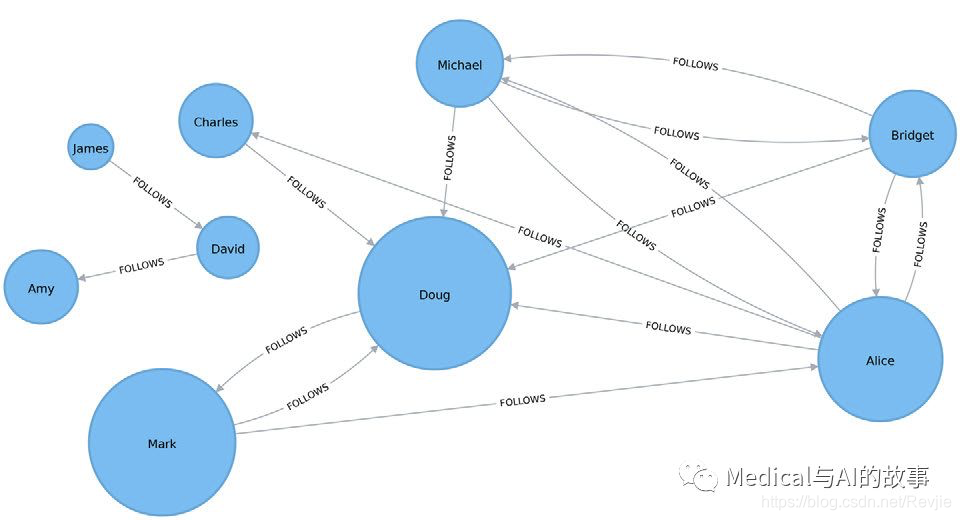图5-13. 页面排名可视化

与Spark示例一样，运行PageRank算法的图中的关系没有权重，因此每个关系都被认为是相等的。通过在传递给PageRank过程的配置中包含weightProperty属性，可以考虑关系权重。例如，如果关系具有包含权重的属性权重，我们将向过程传递以下配置：weightProperty: “weight”。

PageRank变体：个性化的PageRank

个性化的PageRank（Personalized PageRank, PPR）是PageRank算法的一种变体，它从特定节点的角度计算图形中节点的重要性。对于PPR，随机跳转（PageRank中15%的随机跳转）指的是跳转回来一系列启动节点。这会使结果偏向开始节点，或使其个性化。这种偏差和本地化使得PPR对于高目标的建议很有用。

Apache Spark上的个性化页面排名

我们可以通过传入sourceId参数来计算给定节点的个性化PageRank得分。以下代码计算Doug的PPR：

me = "Doug"
results = g.pageRank(resetProbability=0.15, maxIter=20, sourceId=me)
people_to_follow = results.vertices.sort("pagerank", ascending=False)
already_follows = list(g.edges.filter(f"src = '{me}'").toPandas()["dst"])
people_to_exclude = already_follows + [me]
people_to_follow[~people_to_follow.id.isin(people_to_exclude)].show()

这个查询的结果可以用来为Doug建议应该关注的人。请注意，我们还确保将Doug已经关注的人以及他自己被排除在我们的最终结果之外。 如果我们在PySpark中运行该代码，我们将看到这个输出：(译者：原书中的这段代码可能无法运行)

+---------+-----------------------+
| id      | pageRank              |
+---------+-----------------------+
| Alice   | 0.1650183746272782    |
| Michael | 0.048842467744891996  |
| Bridget | 0.048842467744891996  |
| Charles | 0.03497796119878669   |
| David   | 0.0                   |
| James   | 0.0                   |
| Amy     | 0.0                   |
+---------+-----------------------+

Alice是Doug最应该关注的人，但我们也可以建议关注Michael和Bridget。

总结

中心性算法是识别网络中影响因素的一个很好的工具。在本章中，我们学习了典型的中心性算法：度中心性、紧密中心性、中介中心性和PageRank。我们还讨论了几个变体来处理诸如长运行时间和独立组件等问题，以及其他用途的选项。

中心性算法有许多广泛的用途，我们鼓励各种分析和探索。你可以运用我们学到的知识，找到传播信息的最佳接触点，找到控制资源流动的隐藏经纪人，并发现隐藏在阴影中的间接权力参与者。

接下来，我们将讨论研究组和分区的社区检测算法。